第一题

题目

假设所分析的数据包括属性 age,它在数据元组中的值（以递增序）为

13 ,15 ,16 ,16 ,19 ,20 ,20 ,21 ,22 ,22 ,25 ,25 ,25 ,25 ,30 ,33 ,33 ,35 ,35 ,35 ,35 ,36 ,40 ,45 ,46 ,52,70。

a. 该数据的均值是多少？中位数是什么？

b. 该数据的众数是什么？讨论数据的模态（即二模、三模等）。

c. 该数据的中列数是多少？

d. 你能（粗略地）找出该数据的第一个四分位数（Q1）和第三个四分位数（Q3）吗？

e. 给出该数据的五数概括。

f. 绘制该数据的盒图。

g. 分位数-分位数图与分位数图有何不同？

解答

a. 平均值：30.15 中位数：31.5

模态指的是一组数据中出现最频繁的数值

b. 众数是25和35 有两模态

中列数是指将数据按升序排列后，取最中间的五个数字的平均数。

c. 中列数：24.4

在统计学中，四分位数是将一组数据分为四个等份的值。四分位数的概念是用于描述数据的分布和形态。通常，我们使用三个四分位数来描述数据的分布，它们分别是：

第一个四分位数Q1：将数据集分为最低的25％，即数据集的前1/4部分。
第二个四分位数Q2：与中位数相同，将数据集分为两个相等的部分，即前50％和后50％。
第三个四分位数Q3：将数据集分为最高的25％，即数据集的后1/4部分。

可以使用排序算法将数据集中的数字按升序排列，然后找到相应的位置来计算四分位数。四分位数是描述数据分布的重要工具，因为它们提供了数据集的分位点，可以用来确定数据集的集中趋势、分散程度以及异常值的存在。

d. Q1=20 Q3=42.5

一个数据集的五数概括指的是该数据集的最小值、第一四分位数Q1、中位数Q2、第三四分位数Q3和最大值，用于描述数据的分布情况。

e. 五数概况：13, 20, 25, 42.5, 70

最小值：13
Q1：20
Q2：25
Q3：42.5
最大值：70

f. 使用python绘图：

盒图通常由五个要素组成：最大值、最小值、中位数、第一四分位数（Q1）和第三四分位数（Q3）。其中，箱体表示数据的四分位数范围（Q1到Q3），箱体中的线表示中位数，箱体上下的“须”表示数据的范围，最终点表示数据中的异常值。

import matplotlib.pyplot as plt

data = [13, 15, 16, 16, 19, 20, 20, 21, 22, 22, 25, 25, 25, 25, 30, 33, 33, 35, 35, 35, 35, 36, 40, 45, 46, 52, 70]

fig, ax = plt.subplots()

ax.boxplot(data, vert=False, widths=0.5, notch=True, patch_artist=True, 
           boxprops=dict(facecolor='#e0e0e0', color='black'), 
           whiskerprops=dict(color='black'), flierprops=dict(marker='o', markersize=3),
           medianprops=dict(color='red', linewidth=1.5))

ax.set_title('Boxplot of Data')
ax.set_xlabel('Value')
ax.set_yticklabels([''])

plt.show()

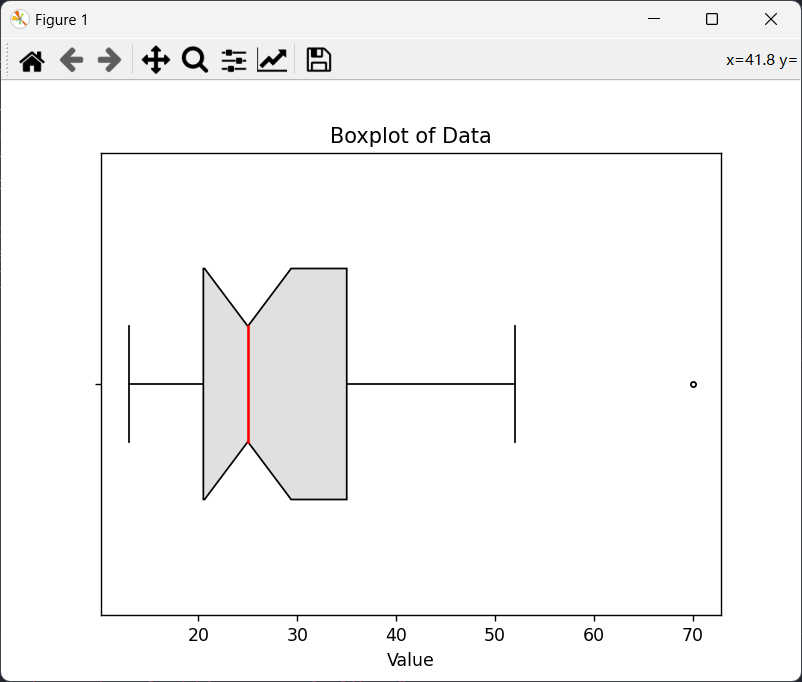
e. 分位数-分位数图（Q-Q Plot）是用于比较两个数据集的分布是否相似的图表，可以判断它们的差异在哪些方面；而分位数图（Box Plot）则用于展示单个数据集的分布情况，能够直观地表示数据的中心趋势、离散程度和异常值情况。

第二题

题目

在数据分析中，重要的选择相似性度量。然而，不存在广泛接受的主观相似性度量，结果可能因所用的相似性度量而异。虽然如此，在进行某种变换后，看来似乎不同的相似性度量可能等价。

假设我们有如下二维数据集：

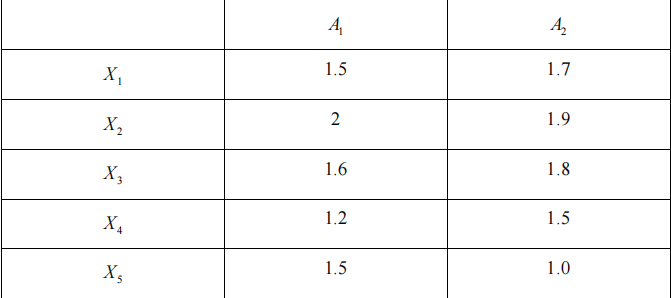
a. 把该数据看做二维数据点。给定一个新的数据点x=(1.4,1.6) 作为查询点，使用欧几里得距离、曼哈顿距离、上确界距离和余弦相似性，基于查询点的相似性对数据库的点排位。

b. 规格化该数据集，使得每个数据点的范数等于 1。在变换后的数据上使用欧几里得距离对诸数据点排位。

解答

a. 解答如下

欧几里得距离（Euclidean Distance）：计算查询点x和每个数据点之间的欧几里得距离，并按照距离从小到大进行排名。欧几里得距离公式为：$\sqrt{\sum_{i=1}^{n}(x_i - y_i)^2}$
- x=(1.4,1.6) 时，每个数据点到查询点的欧几里得距离分别为：
  - X1: $\sqrt{(1.5-1.4)^2 + (1.7-1.6)^2} \approx 0.141$
  - X2: $\sqrt{(2-1.4)^2 + (1.9-1.6)^2} \approx 0.640$
  - X3: $\sqrt{(1.6-1.4)^2 + (1.8-1.6)^2} \approx 0.282$
  - X4: $\sqrt{(1.2-1.4)^2 + (1.5-1.6)^2} \approx 0.223$
  - X5: $\sqrt{(1.5-1.4)^2 + (1-1.6)^2} \approx 0.640$
- 按照距离从小到大排名：X1 > X4 > X3 > X2, X5
曼哈顿距离（Manhattan Distance）：计算查询点x和每个数据点之间的曼哈顿距离，并按照距离从小到大进行排名。曼哈顿距离公式为：$\sum_{i=1}^{n} |x_i - y_i|$
- x=(1.4,1.6) 时，每个数据点到查询点的曼哈顿距离分别为：
  - X1: $|1.5-1.4| + |1.7-1.6| \approx 0.2$
  - X2: $|2-1.4| + |1.9-1.6| \approx 0.9$
  - X3: $|1.6-1.4| + |1.8-1.6| \approx 0.4$
  - X4: $|1.2-1.4| + |1.5-1.6| \approx 0.3$
  - X5: $|1.5-1.4| + |1-1.6| \approx 0.7$
- 按照距离从小到大排名：X1 > X4 > X3 > X2, X5
上确界距离（Chebyshev Distance）：计算查询点x和每个数据点之间的上确界距离，并按照距离从小到大进行排名。上确界距离公式为：$\max_{i=1}^{n} |x_i - y_i|$
- x=(1.4,1.6) 时，每个数据点到查询点的上确界距离分别为：
  - X1: $\max(|1.5-1.4|, |1.7-1.6|) \approx 0.1$
  - X2: $\max(|2-1.4|, |1.9-1.6|) \approx 0.6$
  - X3: $\max(|1.6-1.4|, |1.8-1.6|) \approx 0.4$
  - X4: $\max(|1.2-1.4|, |1.5-1.6|) \approx 0.2$
  - X5: $\max(|1.5-1.4|, |1-1.6|) \approx 0.6$
- 按照距离从小到大排名：X1 > X4 > X3 > X2, X5
余弦相似性（Cosine Similarity）：计算查询点x和每个数据点之间的余弦相似度，并按照相似度从大到小进行排名。余弦相似度公式为：$\frac{\sum_{i=1}^{n}x_i y_i}{\sqrt{\sum_{i=1}^{n}x_i^2}\sqrt{\sum_{i=1}^{n}y_i^2}}$
- x=(1.4,1.6) 时，每个数据点与查询点的余弦相似度分别为：
  - X1: $\frac{(1.5\times1.4)+(1.7\times1.6)}{\sqrt{(1.5^2+1.7^2)\times(1.4^2+1.6^2)}} \approx 0.997$
  - X2: $\frac{(2\times1.4)+(1.9\times1.6)}{\sqrt{(2^2+1.9^2)\times(1.4^2+1.6^2)}} \approx 0.990$
  - X3: $\frac{(1.6\times1.4)+(1.8\times1.6)}{\sqrt{(1.6^2+1.8^2)\times(1.4^2+1.6^2)}} \approx 0.997$
  - X4: $\frac{(1.2\times1.4)+(1.5\times1.6)}{\sqrt{(1.2^2+1.5^2)\times(1.4^2+1.6^2)}} \approx 0.985$
  - X5: $\frac{(1.5\times1.4)+(1\times1.6)}{\sqrt{(1.5^2+1^2)\times(1.4^2+1.6^2)}} \approx 0.939$
- 按照相似度从大到小排名：X1 > X3 > X2 > X4 > X5

为了规格化数据集中的每个数据点，我们需要计算每个数据点的范数，然后将每个数据点除以其范数即可。范数是指向量的长度，对于二维向量 $(x_1, x_2)$ 的范数，即为 $\sqrt{x_1^2 + x_2^2}$。

首先，计算每个数据点的范数：

Data Point	$L_2$ Norm
X1	$\sqrt{1.5^2 + 1.7^2} \approx 2.311$
X2	$\sqrt{2^2 + 1.9^2} \approx 2.776$
X3	$\sqrt{1.6^2 + 1.8^2} \approx 2.355$
X4	$\sqrt{1.2^2 + 1.5^2} \approx 1.922$
X5	$\sqrt{1.5^2 + 1^2} \approx 1.802$

然后，将每个数据点除以其范数，得到规格化后的数据集：

Data Point	A1 (Normalized)	A2 (Normalized)
X1	0.648	0.761
X2	0.720	0.694
X3	0.677	0.736
X4	0.628	0.778
X5	0.835	0.550

现在，我们可以使用欧几里得距离对规格化后的数据集中的数据点进行排名。计算查询点 x=(1.4,1.6) 与每个数据点之间的欧几里得距离，并按照距离从小到大进行排名。欧几里得距离公式为：$\sqrt{\sum_{i=1}^{n}(x_i - y_i)^2}$。

x=(1.4,1.6) 时，每个数据点到查询点的欧几里得距离分别为：
- X1: $\sqrt{(0.648-1.4)^2 + (0.761-1.6)^2} \approx 0.824$
- X2: $\sqrt{(0.72-1.4)^2 + (0.694-1.6)^2} \approx 0.732$
- X3: $\sqrt{(0.677-1.4)^2 + (0.736-1.6)^2} \approx 0.716$
- X4: $\sqrt{(0.628-1.4)^2 + (0.778-1.6)^2} \approx 0.914$
- X5: $\sqrt{(0.835-1.4)^2 + (0.55-1.6)^2} \approx 0.864$
按照距离从小到大排名：X3 > X2 > X5 > X1 > X4

第三题

问题

使用如下方法规范化如下数组：

200，300，400，600, 1000

a. 令 min=0，max=1，最小—最大规范化。

b. z 分数规范化。

c. z 分数规范化，使用均值绝对偏差而不是标准差。

d. 小数定标规范化。

解答

a. 步骤：

找到数据中的最小值和最大值。
使用以下公式将每个数据点规范化为0到1之间的值：

规范化后的值 = (原始值 - 最小值) / (最大值 - 最小值)

原始值 | 规范化后的值

200 | 0

300 | 0.111

400 | 0.222

600 | 0.444

1000 | 1

b. 步骤：

计算数据的平均值和标准差。
使用以下公式将每个数据点规范化为平均值为0，标准差为1的z分数：

规范化后的值 = (原始值 - 平均值) / 标准差

原始值 | 规范化后的值

 200 | -1.15

300 | -0.77

400 | -0.39

600 | 0.77

1000 | 1.54

z分数规范化是一种将数据点映射到标准正态分布的方法，即平均值为0，标准差为1。

c. 步骤：

计算数据的平均值和均值绝对偏差（MAD）。
1. 计算均值绝对偏差（MAD）的步骤如下：
  1. 首先计算数据的平均值。
  2. 对于每个数据点，计算它与平均值的差的绝对值。
  3. 将所有这些绝对值相加并求平均值，即：
  MAD = （|X1 - mean| + |X2 - mean| + … + |Xn - mean|） / n
其中，n是数据点的数量，X1、X2、…、Xn表示每个数据点的值。
使用以下公式将每个数据点规范化为平均值为0，均值绝对偏差为1的z分数：

规范化后的值 = (原始值 - 平均值) / MAD

原始值 | 规范化后的值

200 | -1.39

300 | -0.93

400 | -0.47

600 | 0.93

1000 | 1.86

z分数规范化使用均值绝对偏差（MAD）而不是标准差来测量数据点与平均值之间的距离。MAD是数据点与平均值之间距离的中位数，它可以提供比标准差更健壮的测量方法，因为它不受异常值的影响。

d. 步骤：

找到这组数据的最大值（在这个例子中是1000）。
确定一个比最大值大的10的幂，使得所有数据点除以该幂后得到的值都在[-1,1]之间。在这个例子中，选择1000作为10的幂。
将每个数据点除以该幂，并向下取整到最接近的整数。这个整数就是小数定标规范化的结果。

原始值 | 规范化后的值

200 | 0.2

300 | 0.3

400 | 0.4

600 | 0.6

1000 | 1

小数定标规范化是一种将数据点转换为小于1的整数的方法，以减小数据点之间的值的大小差异。规范化后的值可以被看作是原始值与幂的次方之间的比率，因此它们可以直接进行比较。小数定标规范化适用于处理小数的计算机程序，因为它可以将小数转换为整数，从而避免了小数计算的误差。

第四题

问题

假设 12 个销售价格记录已经排序，如下所示：

5，10，11，13，15，35，50，55，72，92，204，215

使用如下各方法将它们划分成三个箱。

a. 等频（等深）划分。

b. 等宽划分。

c. 聚类

解决

a. 等频（等深）划分

等频（等深）划分法是将数据按照数量相等的方式分成多个组。

确定要分成的组数n，例如本题中是3组。
计算每组的数据个数k，即将数据总数除以组数，向下取整。在本题中，数据总数为12，所以每组的数据个数为4个。
将数据按照从小到大的顺序排序，然后将前k个数据放入第一组，接下来的k个数据放入第二组，以此类推，直到所有数据都被放入其中一个组中。

箱子1：5，10，11，13
箱子2：15，35，50，55
箱子3：72，92，204，215

b. 等宽划分

等宽划分法是将数据按照数值范围相等的方式划分成多个组。

确定要分成的组数n，例如本题中是3组。
计算数据的数值范围R，即最大值减去最小值。在本题中，R=215-5=210。
计算每组的数值范围W，即将数据的数值范围R除以组数，向上取整。在本题中，W=70。
将最小值作为第一组的下限，第一组的上限为下限加上W；第二组的下限为第一组的上限加1，上限为下限加上W；以此类推，直到所有组的上限被确定为止。

箱子1：5-74
箱子2：75-144
箱子3：145-215

c. 聚类

聚类法是一种基于数据相似度进行分组的方法，它将数据划分为若干个子集，使得每个子集内部的数据相似度尽可能高，不同子集之间的数据相似度尽可能低。

选择一种聚类算法，例如K-Means算法、层次聚类算法等。这里以K-Means算法为例进行说明。
确定要分成的聚类数k，例如本题中是3个聚类。
随机选取k个点作为聚类中心。
将每个数据点分配到最近的聚类中心所在的聚类中。
计算每个聚类的新的中心点，即将该聚类内部所有点的坐标求平均得到的点。
如果聚类中心点发生变化，则重复步骤4-5，直到聚类中心点不再发生变化为止。

簇1：5，10，11，13，15，35
簇2：50，55，72，92
簇3：204，215

计算距离

首先，需要计算每个数据点与3个聚类中心点之间的距离。这里采用欧式距离作为距离度量方法。以第1个数据点为例，计算其与3个聚类中心点之间的距离如下：
- 与第1个中心点的距离：sqrt((5-5)^2) = 0
- 与第6个中心点的距离：sqrt((5-35)^2) = 30
- 与第11个中心点的距离：sqrt((5-204)^2) = 199
同样的，可以计算出其他数据点与3个聚类中心点之间的距离。
分配簇

根据距离计算结果，将每个数据点分配到距离最近的簇中。例如，根据上面计算得到的距离，可以将数据点分配到以下3个簇中：
- 簇1：5，10，11，13
- 簇2：15，35，50，55
- 簇3：72，92，204，215
计算新的聚类中心点

对于每个簇，计算其内部数据点的均值，作为该簇的新聚类中心点。例如，在本题中，可以计算出每个簇的平均值，然后将其作为新的聚类中心点。具体计算如下：
- 簇1的平均值为 (5+10+11+13)/4 = 9.75
- 簇2的平均值为 (15+35+50+55)/4 = 38.75
- 簇3的平均值为 (72+92+204+215)/4 = 145.75
更新聚类中心点

将新的聚类中心点作为簇的中心点，重复步骤1-3，直到每个簇的中心点都不再发生变化。例如，在第一轮迭代中，新的聚类中心点为第2个、第7个和第12个数据，分配结果如下：
- 簇1：5，10，11，13
- 簇2：15，35，50
- 簇3：55，72，92，204，215
然后再计算新的聚类中心点，直到每个簇的中心点不再发生变化。